Perfect competition provides
a benchmark against which the behavior of
other market is judged. Even though perfect
competition is rarely, if ever, encountered
in the real world, we study the perfect competition
model because it provides an ideal against
which other models (cooperative and noncooperative
oligopoly and duopoly, monopoly) and markets
are compared.
The main assumptions of perfect
competition are :
| Homogeneous
Good |
All firms
sell an identical product. Consumers view
the products of various firms as the same,
hence, are indifferent between them |
| Perfect information |
Buyers ans sellers have
all relevant information about the market
including the price and quality of the
product |
| Price Taking |
Buyers
and sellers cannot individually influence
the price at which the product can be
purchased or sold. Price is determined
by the market, so each buyer takes the
price as given |
| No transaction
Costs |
Neither
buyers nor sellers incur costs or fees
to participate in the market |
| Free Entry and
Exit |
Firms
can enter and exit the industry quickly
at any time without having to incur any
special expense. That is, firms do not
face barriers to entry or exit |
Some economists also assume
that a perfectly competitive market has a
large number of buyers and sellers.
If there are many firms, no
one firm can charge a price above the market
price without losing all
its customers, so
the firm views the price at which it can sell
as beyond its control.
Similarly,
consumers cannot find a firm willing to sell
below the market price, so consumers must
view the market price as beyond their control.
Even if there
are relatively few firms in an industry, no
firm could raise its price above the market
price without losing all its customers if
another firm could quickly enter the industry
and underprice it.
Thus, because
we assume firms and consumers are price takers
and that there is free entry and exit, we
do not also make the assumption that there
are a large number of firms.
Competitive
markets typically have a large number of firms
and consumers, but some industries have all
the properties of perfect competition even
though there are few firms in those industries.
Profit
maximization
The objective of any firm, including
a competitive firm, is to maximize its profits.
As a result of the price-taking
assumption above, the firm can sell all it
wants at price "p". The firm is
too smale to influence the market price. That
is, the firm faces a horizontal demand curve
at price "p".
If it is profitable for the
firm to expand output as long as the extra
revenue (price or marginal revenue) from selling
an additional unit exceeds the extra cost
(marginal cost) of producing that unit.
The profit is maximum when
Price vs Marginal
cost
|
Marginal
profit |
Total
Profit |
| Price |
> |
Marginal
cost |
positive |
increases |
| Price |
= |
Marginal cost |
0 |
maximum |
Price |
< |
Marginal cost |
negative |
decreases |
Example : results of a competitive
firm
q |
TC |
R |
Profit |
Marginal |
MC |
Price |
- |
128'000 |
- |
-128'000 |
|
69.00 |
60.00 |
1'000 |
184'000 |
60'000 |
-124'000 |
16.00 |
44.00 |
60.00 |
2'000 |
218'000 |
120'000 |
-98'000 |
35.00 |
25.00 |
60.00 |
3'000 |
236'000 |
180'000 |
-56'000 |
48.00 |
12.00 |
60.00 |
4'000 |
244'000 |
240'000 |
-4'000 |
55.00 |
5.00 |
60.00 |
5'000 |
248'000 |
300'000 |
52'000 |
56.00 |
4.00 |
60.00 |
6'000 |
254'000 |
360'000 |
106'000 |
51.00 |
9.00 |
60.00 |
7'000 |
268'000 |
420'000 |
152'000 |
40.00 |
20.00 |
60.00 |
8'000 |
296'000 |
480'000 |
184'000 |
23.00 |
37.00 |
60.00 |
9'000 |
344'000 |
540'000 |
196'000 |
- |
60.00 |
60.00 |
10'000 |
418'000 |
600'000 |
182'000 |
-29.00 |
89.00 |
60.00 |
11'000 |
524'000 |
660'000 |
136'000 |
-64.00 |
124.00 |
60.00 |
12'000 |
668'000 |
720'000 |
52'000 |
-105.00 |
165.00 |
60.00 |
12'452 |
747'120 |
747'120 |
0 |
|
|
60.00 |
13'000 |
856'000 |
780'000 |
-76'000 |
-152.00 |
212.00 |
60.00 |
Empirical approach
Empirically we observe that
the competitive firm output which maximizes
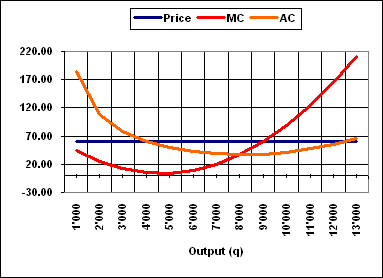
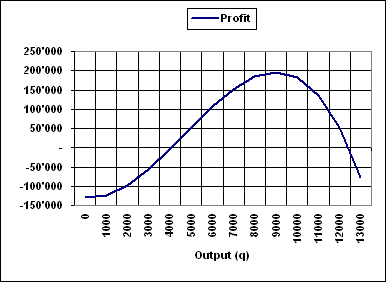
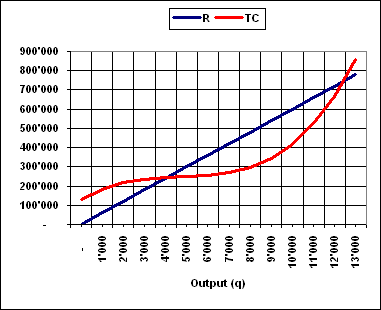
its profit is 9.000 at a market price of 60 € (do not change)
The profit of the firm is maximum
when
| market
price |
= |
Marginal
Cost (MC) |
MC = Variation of Total Cost
when output varies of one unit.
| Output
(q) |
Price |
MC |
Marginal
profit |
| 8000 |
60.00 |
37.00 |
32.00 |
| 9000 |
Price
= MC |
0 |
|
10000 |
60.00 |
89.00 |
-14.00 |
Scientifical
approach
Market price : 60 €
Revenue
Function : R = f(q) = pq = 60q
Total Cost Function
: TC = 0.000001q3 - 0.014q2 + 69q + 128'000
- Output : q
- Fixed cost : 128'000
- Variable cost : VC = 0.000001q3 - 0.014q2 + 69q
Tool
to find "Total cost function" :
Excel "Tools / Data analysis / Regression"
Marginal Cost Function : MC = 0.000003q2 - 0.028q + 69 (derivated of the TC function)
Average Cost Function : AC = TC / q = 0.000001q2- 0.014q + 69 + (128'000 / q)
Profit Function : Profit =(R - C) = 60q - ( 0.000001q3- 0.014q2 + 69q + 128'000 )
Profit = - 0.000001q3+ 0.014q2 - 9q - 128'000
Marginal Profit Function : Profit' = - 0.000003q2+ 0.028q - 9 (derivated of the Profit Function)
Calculations
For which output Price = MC ?
( P - MC ) = 0,000003q2 - 0,028q + 9 = 0
Formula to solve this equation :
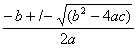
Optimum output : 9'000
units
|
Optimum
Output |
Revenue |
Total
Cost |
Maximum
Profit |
Price |
MC |
| 9'000 |
540'000 |
344'000 |
196'000 |
60.00 |
60.00 |
Strategies for a competitive
firm to be more efficient
Sources :
Modern Industrial Organization, 2nd edition, Dennis .W. Carlton , Jeffrey .M. Peroloff, Addfison-Wesley, 1994
Economie Industrielle ( traduction de la 2ème édition par Fabrice Mazerolle), Dennis .W. Carlton , Jeffrey .M. Peroloff, de Boeck Université, 1998
Cours de Microéconomie,
Bernard Jaquier, Ecole Hôtelière
de Lausanne, 2003
(c) Bernard Jaquier, Professor in Economics and Finance, Ecole Hôtelière de Lausanne, Switzerland, 2018