MONOPOLY
A firm is a monopoly if it
is the only supplier of a product for which
there is no close substitute. A monopoly sets
its price without fear that it will be undercut
by a rival firm. A monopoly faces a downward-sloping
demand curve and sets a price above marginal
cost. As a result, less is sold than if the
market were competitive (price = marginal
cost) and there is deadweight loss to society.
Profit maximization
Like a competitive firm, a monopoly
sets its level of output to maximize its profit.
Because the demand curve is downward sloping,
the more the monopoly sells, the lower the
price it receives.
Because the tradeoff between
price and quantity is completely determined
by the market demand curve, the monopoly,
in its quest to maximize profits, can set
only price or only quantity - not both.
If the monopoly sets quantity,
the market price is determined by the market
demand curve.
If it sets price, the quantity
is determined by the market demand curve.
Example : results of a monopoly
Data of the firm |
Calculations |
q |
TC |
R |
Profit |
MC |
R' |
Profit' |
0 |
128'000 |
- |
-128'000 |
|
|
|
1000 |
184'000 |
185'000 |
1'000 |
56.00 |
185.00 |
129.00 |
2000 |
218'000 |
350'000 |
132'000 |
34.00 |
165.00 |
131.00 |
3000 |
236'000 |
495'000 |
259'000 |
18.00 |
145.00 |
127.00 |
4000 |
244'000 |
620'000 |
376'000 |
8.00 |
125.00 |
117.00 |
5000 |
248'000 |
725'000 |
477'000 |
4.00 |
105.00 |
101.00 |
6000 |
254'000 |
810'000 |
556'000 |
6.00 |
85.00 |
79.00 |
7000 |
268'000 |
875'000 |
607'000 |
14.00 |
65.00 |
51.00 |
8000 |
296'000 |
920'000 |
624'000 |
28.00 |
45.00 |
17.00 |
9000 |
344'000 |
945'000 |
601'000 |
48.00 |
25.00 |
-23.00 |
10000 |
418'000 |
950'000 |
532'000 |
74.00 |
5.00 |
-69.00 |
11000 |
524'000 |
935'000 |
411'000 |
106.00 |
-15.00 |
-121.00 |
12000 |
668'000 |
900'000 |
232'000 |
144.00 |
-35.00 |
-179.00 |
13000 |
856'000 |
845'000 |
-11'000 |
188.00 |
-55.00 |
-243.00 |
Empirical approach
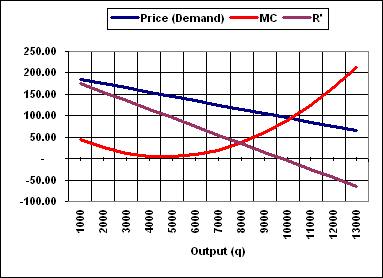
Empirically we observe that
the monopoly output which maximizes its profit
is 8.000 at a market price of 115.00 (Revenue
/ Output)
The profit of the monopoly is
maximum when
| Marginal
Revenue (R') |
= |
Marginal
Cost (MC) |
MR = Variation of Revenue when
output varies of one unit. MC = Variation
of Total Cost when output varies of one unit.
| Output
(q) |
R' |
MC |
Marginal
profit |
| 6000-7000 |
65.00 |
14.00 |
51.00 |
| 7000-8000 |
45.00 |
28.00 |
17.00 |
| ? |
R'
= MC |
0 |
| 8000-9000 |
25.00 |
48.00 |
-23.00 |
Scientifical
approach
Tool
: Excel "Tools / Data analysis / Regression"
Revenue
function : R = f(q) = pq = - 0.01q2 +
195q
- Price function : p = f(q)
= [R / q] = - 0.01q + 195
- Demand function : q = f(p)
= 19.500 - 100p
- R' function : R' = - 0,02q
+ 195
Total cost function
: TC = 0.000001q3- 0.014q2 + 69q + 128'000
- Marginal cost function :
MC = 0.000003q2 - 0.028q + 69
Calculations
For which output R' = MC ?
(R' - MC) = 0.000003q2 + 0.008q + 126
Formula to solve this equation :
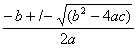
Optimum output : 7'950
units
| Optimum
Output |
Revenue |
Total
Cost |
Maximum
Profit |
Optimum
Price |
MR |
MC |
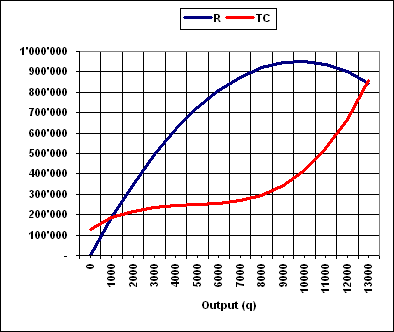
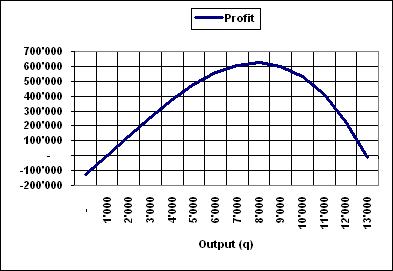
| 7'950 |
918'225 |
294'175 |
624'050 |
115.50 |
36.00 |
36.00 |
Figures
Sources
:
Modern Industrial Organization, 2nd edition, Dennis .W. Carlton , Jeffrey .M. Peroloff, Addfison-Wesley, 1994
Economie Industrielle ( traduction de la 2ème édition par Fabrice Mazerolle), Dennis .W. Carlton , Jeffrey .M. Peroloff, de Boeck Université, 1998
Cours de Microéconomie,
Bernard Jaquier, Ecole Hôtelière
de Lausanne, 2003
(c) Bernard Jaquier, Professor in Economics and
Finance, Ecole Hôtelière de Lausanne,
Switzerland, 2018